Ellipsoid Method

In this article, I will give a brief guide on what the ellipsoid method is. A good reference would be the note by Sébastien Bubeck ¹.

I will first give a high-level breakdown on why this algorithm works, then briefly write about how mathematically the ellipsoids are manipulated. Another optimization algorithm that is seldomly used in practice, but conceptually closely-related is the center of gravity method. This is explored here.

1. Setting the Stage#

1.1. Assumptions and Notations#

Optimization Problem. Minimize a convex function defined over a convex body .

General results on convex analysis guarantees that attains minimum on some ; let us also write the optimal value as .

Assumptions. For , we make the assumptions:

1. Value Bound. for some .
2. Volume Bound. for some , ; here is the open ball centered at with radius .

Available Oracles. We assume the following 0th and 1st-order oracles available to us:

1. Separation Oracle. Given , we can ask for a direction with , where is the half space .
2. Subgradient Oracle. Given , we can ask for a direction .

1.2. Utilizing Volume and Value Bounds via Shrinking#

Intuitively, points close to shouldn’t be too bad. Although we do not know , it still makes sense to consider the following construction: Given , define the set (which can be thought of shrinking towards ):

On this set, we have the function bounds and volume bounds on :

by utilizing our assumptions on convexity, volume and value bounds. In this sense, we have the following general idea:

If we are able to solve for an optimal point in a major portion of the feasibility region, this point would in fact be close to the true optimal solution.

We formalize this idea and give an abstract proof of why the ellipsoid method works.

1.3. General Proof of Convergence#

The ellipsoid method is an iterative method. In each step, it gains total control of a part of the feasibility region, by using ellipsoids as a proxy, through halving along subgradients or separating hyperplanes.

Suppose at time , the remaining uncontrolled region is written as . This gives us a descending sequence of subsets:

As an old adage goes:

To control an onion, all you have to do is to control its peels.

we mathematically express , where are the peels, and formulate strategies to control .

Now for each set , say we have a point with either , or with , then by taking , and assuming , we in fact have . For a proof, note that for any , the volume bounds on shows that cannot contain for large enough , while we have:

The following diagram might be useful for navigating the definitions and symbols (coutesy to draw.io)

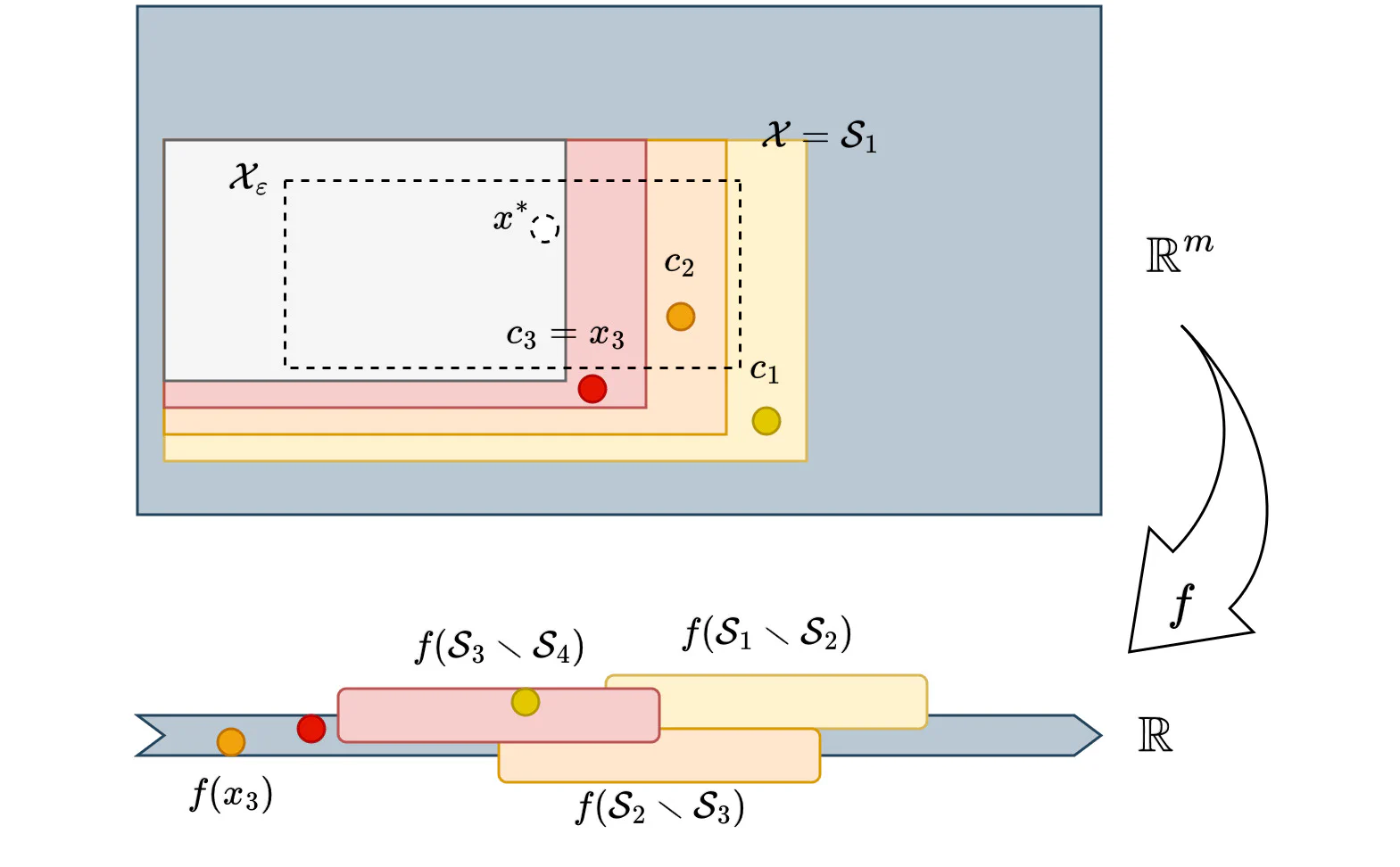
In optimization, we are also interested in the question of the speed of convergence. By using the same idea for estimation, we see that it depends on . In ellipsoid methods - as one can guess it - these are given by manipulations with ellipsoids; in center of gravity methods, these are given by other means.

1.4. Using Ellipsoids and Subgradients#

It is now (finally 😅) the time to introduce the ellipsoid algorithm. The steps are as follows:

• Initiallize: Ellipsoid , , ,
• Halving:
  • If , call separation oracle for a nonzero direction , so that
  • Else call subgradient oracle for a direction . If , optimality condition reached, terminate. Otherwise continue.
• Update: Update via the explicit formulas in the next section, to have the properties: and update:
  • to be the new center of this ellipsoid.
  • the argmin of if ; else set to .
  • .
  • .

Note that the sets and points then satisfies the settings we previously introduced that will lead to convergence. With a bit of algebra, one has the following:

Ellipsoid Method: Feasibility and Convergence

For , we have , with:

A bit of interpretation on this result, which would illustrate some cool characteristics of this algorithm:

1. The analytical complexity (that is, the number of calls to the oracles needed) to guarantee an accuracy to is , from a black-box optimization perspective.
2. In such sense, it is a dimension-dependent algorithm - as dimension grows, the calls needed grows.
3. As one can see later, the cost update are just some matrix-vector multiplications, as opposed to center-of-gravity which although have a better analytical complexity (of ), but each time step requires the computation of a nontrivial integral, in which in the most easy cases exact solvers still needs exponential computation time.

2. Ellipsoidal Shenanigans#

Now let us look at some technical tools and results that allow us to work with ellipsoids, tying together the lose ends introduced in the algorithm above.

It is just a brief note on how the math is done, leaving out much of the book-keeping and formula derivations. For even more casual readers, you have already understand what ellipsoid method does🎉!

2.1. Representation of an Ellipsoid#

An ellipsoid is an affine image of . It can be represented as:

where is SPD (symmetric positive definite) (assuming it having positive volume), admitting a decomposition ; such then describes as , hence an ellipsoid.

2.2. “Ellipsoiding” Halved Ellipsoids#

Here is a fun problem in geometry:

The case is trivial, so we assume .

It would be illustrative to work out the case where , and , then map it back using . We want and lie in , so we define:

with ; note that , for . By this requirement, we formulate the optimization problem:

After expressing via , we have by calculus that the optimal point is with value:

After taking account the rescaling of and the remapping of points , we get:

Ellipsoid Update Formula

For , we get:

where: